直角三角形は簡単に計算できるけど…
直角三角形の面積は、学校で習ったとおり
底辺 × 高さ ÷ 2
で求められます。
しかし、直角ではない三角形の場合、この計算式だけでは面積を求められません。
そんなときに役立つのが 「ヘロンの公式」 です。
三角形の 3辺の長さが分かれば、角度を知らなくても面積を計算できる のが大きな特徴です。
ちなみに、面積を表す記号は S。
単位は cm² や m² などを使います。
ヘロンの公式の使い方(基本編)
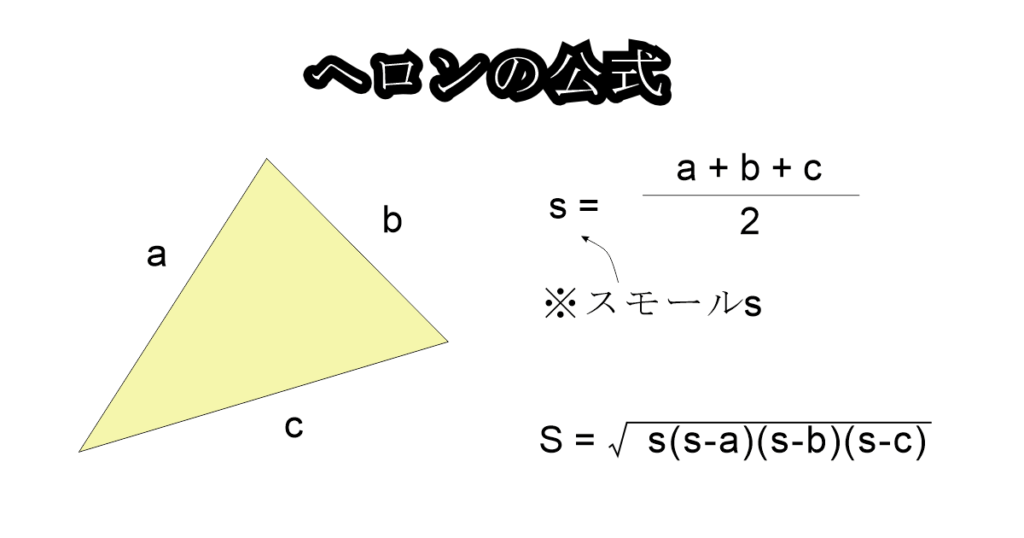
次のように、辺の長さが a / b / c の三角形を考えます。
角度は不明でもかまいません。
まず、予備計算として s を求めます。
s = (a + b + c) / 2
これは三辺の合計を2で割った値です。次に、この s を使って面積 S を計算します。
S = √{ s × (s - a) × (s - b) × (s - c) }
これがヘロンの公式です。
電卓やスマートフォンでも簡単に計算できます。
エクセルでヘロンの公式を使う方法(実務向け)
建設工事や設計の現場では、ヘロンの公式を何度も使うことがあります。
複数の三角形の面積を計算して合計する場合、エクセル(表計算ソフト) が便利です。
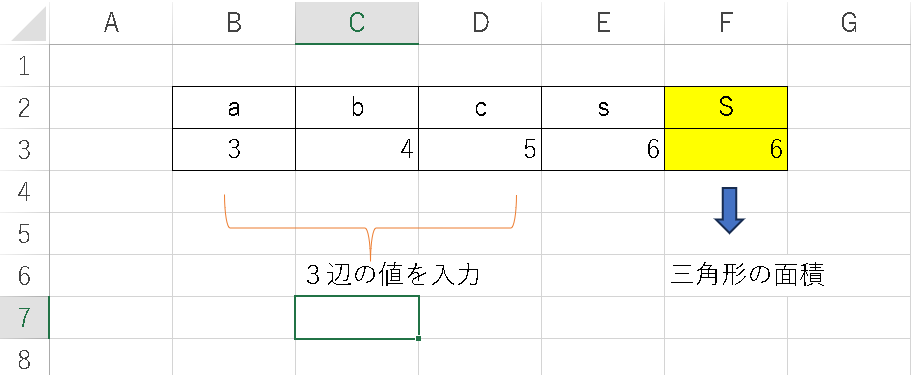
例えば以下のように入力すると、自動で計算できます。
- B3セル:辺 a の値を入力
- C3セル:辺 b の値を入力
- D3セル:辺 c の値を入力
- E3セル:s(スモール s)を計算する数式
- F3セル:最終的な面積 S を計算する数式
数式例
- E3セル:
=(B3+C3+D3)/2
- F3セル:
=SQRT(E3*(E3-B3)*(E3-C3)*(E3-D3))
もし
a = 3、b = 4、c = 5
を入力すると、面積は 6 になれば正解です。
複数の三角形を計算したいときは、4行目以降に数式をコピーすればOKです。
まとめ
- 直角でない三角形も ヘロンの公式 で面積が求められる
- 公式は「sを計算 → 面積Sを計算」の2ステップ
- エクセルを使えば複数の面積を一気に計算できる
「3辺の長さしか分からないけど面積を知りたい!」
そんなときに役立つのが、このヘロンの公式です。




